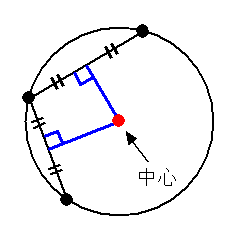
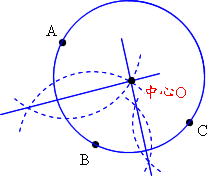
円の中心は求められます。 (1点ではありませんが) 2点の垂直2等分線上に中心があればいいので 垂直2等分線の方程式が円の中心の軌跡 (中心が満たすべき方程式)です。 球の中心の求め方 前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。 球については、表面上にある4点の座標が指定されたら形状が確定します。 (3点の座標と半径 求める円の中心は、\((−2, 0)\) と \((1, 0)\) の中点なので、 \(\displaystyle \left( \frac{−2 1}{2}, \frac{0 0}{2} \right) = \left( −\frac{1}{2}, 0 \right)\) 直径が \(3\) なので、半径は \(\displaystyle \frac{3}{2}\) ゆえに、円の方程式は \((x − a)^2 (y − b)^2 = r^2\)
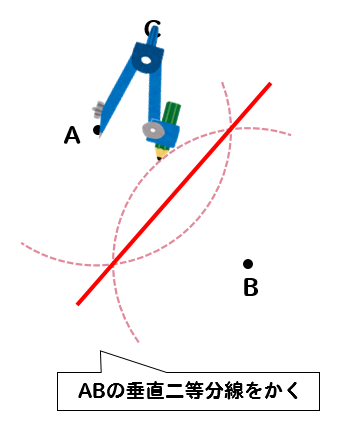
中1 作図 円の中心を求める方法を解説 数スタ
円 中心 求め方 3点
円 中心 求め方 3点- 直角に回転したパスの交わるところが円の中心になっているはずです。 本当でしょうか? 選択ツールで円を選択します。 きちんと円の中心と直線パスの交差しているところが円の中心だとわかりますね。 さてここからが本題です。 計算公式円柱の体積の求め方がわかる2ステップ 中3数学 簡単作図相似の中心を使って拡大図をかく5つのステップ 中3数学 簡単公式直角二等辺三角形の辺の長さの2つの求め方 中3数学 3分でわかる!円周角の定理の逆の証明
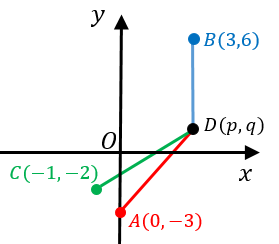



3点を通る円の方程式の2通りの求め方と検算方法 具体例で学ぶ数学
From灘 「円の中心の求め方」 – 朝日小学生新聞 中学受験eye 関西圏 From 進学校 16年9月5日 From灘 「円の中心の求め方」 私は現在、中学1年生に図形の性質を教えています。 定規とコンパスで図形をかく方法を説明した後に、「三角形ABCの三つの頂点を こんにちは。 da Vinch (@mathsouko_vinch)です。この記事のトピックは「円の接線の方程式の公式とその派生系、および使い方」です。 円の接線はどうやって求めればいいのか円と直線の関係を学んだときに円と直線が接する場合円の上で 右クリック して、そのまま3時方向にドラッグします。 クロックメニューが現れたら、マウスボタンを放すと中心点が表示されます。。 ※ ドラッグとは マウスのボタンを押さえたまま、マウスを移動させる操作のことです。
円の円周と扇の弧の長さは等しい 円錐の中心角の求め方は、 扇部分の半径・弧の長さを求める (扇の中心角を求める問題になる) 中心角を求める はかせちゃん 今日もお疲れ様でした! 抹茶ラテ飲んでゆっくりしましょ~ 関連記事はこちら 中学数学外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円中点の座標の求め方 ①与えられた直線に垂直で中心を通る 直線をつくる。 ②①で作った直線と与えられた直線の 交点が弦の中点の座標となる。 円の接線の方程式に関する取り扱い 原点中心・円上の点があたえられたとき x y r円 2 2 2 上の点 a b, における接線の方程式は ax by r 2 原点中心・円外
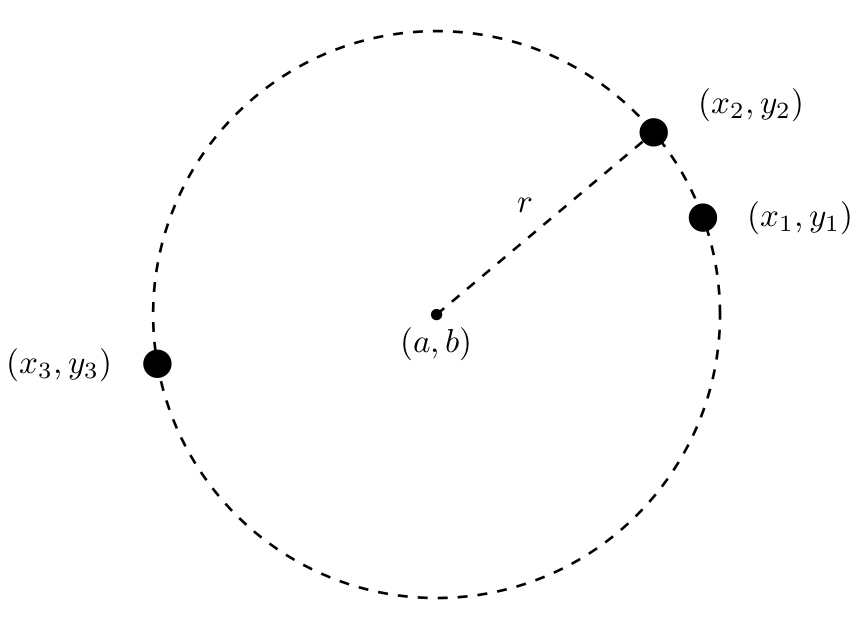
もうアニメを見ただけで手順の解説など必要ないでしょうから注意点だけ紹介しておきます。 アニメの②~③にかけてで 円を選択した後もマウスをホールドしたまま 、3時方向にドラッグするところが今回の円の中心点を出す一番注意すべきところです。 3点を通る円 円は一直線上ではない3点の座標があれば一意に決定します。 下図を参照してください。ここで、3点の座標を、 (x1, y1), (x2, y2), (x3, y3) 求める中心座標を、 (Cx, Cy) 求める半径を、 r とします。 ごく普通に3つの連立方程式を解いていきます参考になるサイトもしくは円の座標の求め方知っている方教えてください ページトップ しろ Re円の座標の求め方 投稿記事 by しろ » 1 year ago 質問者の「円の座標」というのがいったいなにを指し示しているのか全くわかりません。 (xa)^2(yb)^2=r^2 のとき中心座標は(a,b)、半径rになります




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト




3点を通る円の方程式の2通りの求め方と検算方法 具体例で学ぶ数学
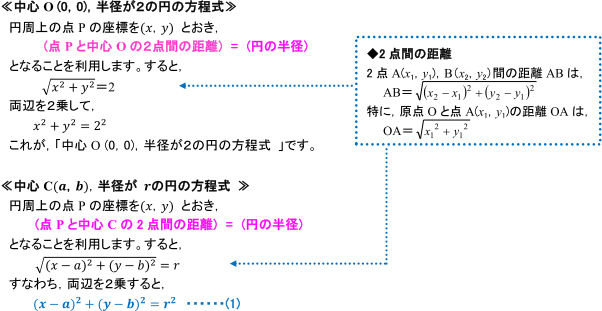
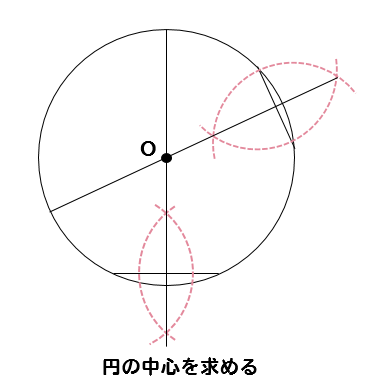
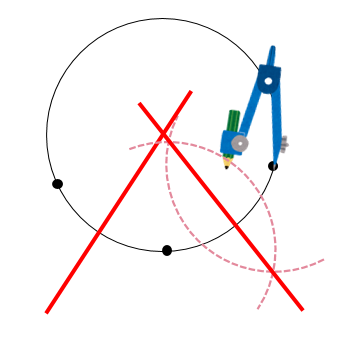
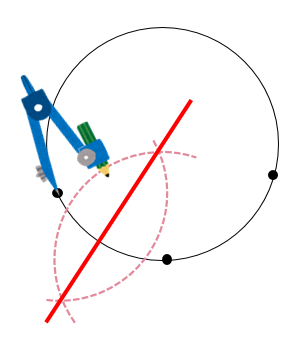
例として,中心が (0, 0) (0,0) (0, 0) で半径が 2 2 2 の円の方程式を考えます。 円の中心を求める まずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 少し大きめの半円を書くよ 周上の他の場所にも、コンパスの針を置いて さっきと同じ大きさの半円を書くよ そして、半円2つが重なった2点を結ぶ線を引くよ 最後に、もう1つ他の周上にコンパスの針を置いて半円を書くよ また線を書いて、すなわち,上記の偏心(a,b)を決定し,それを中心と した同心円でワーク形状を挟んだ場合の半径差が真円度と なることを意味している. 5.真円度と基準円 真円度の求め方には,基準円を元に以下の4つの方法が ある3). 1.最小領域真円度/最小領域基準円 2.最小二乗真円度/最小二乗



2 つの円の位置関係 思考力を鍛える数学
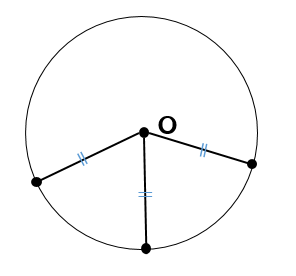



中1 作図 円の中心を求める方法を解説 数スタ
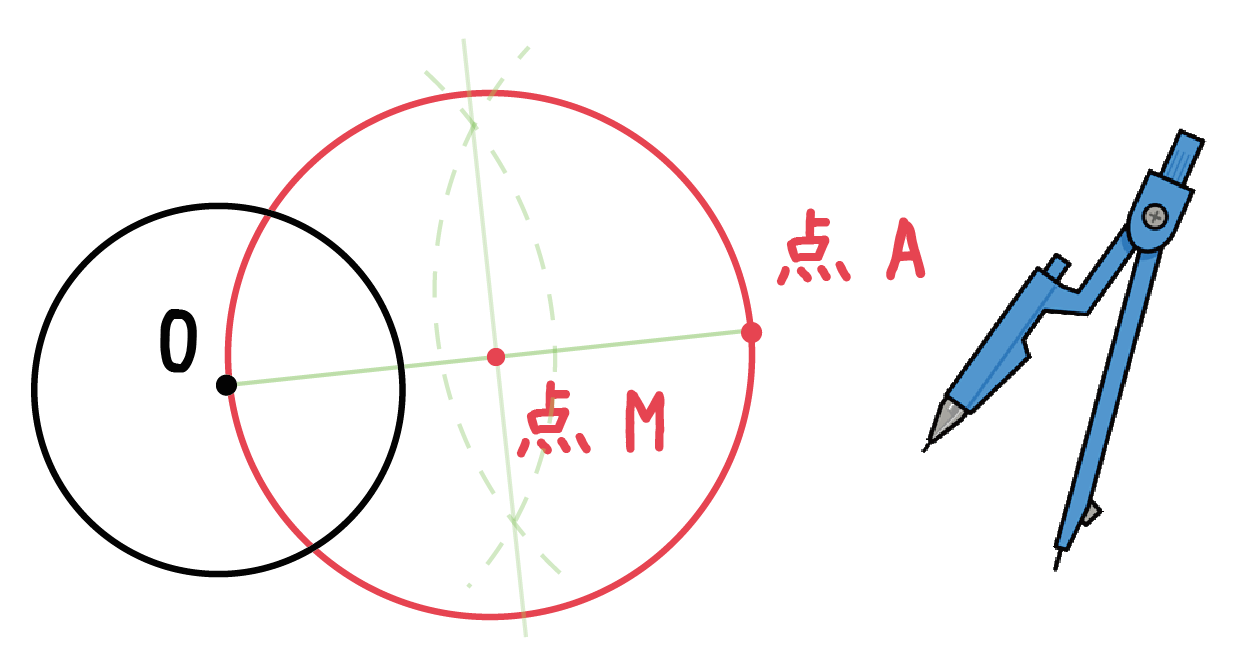
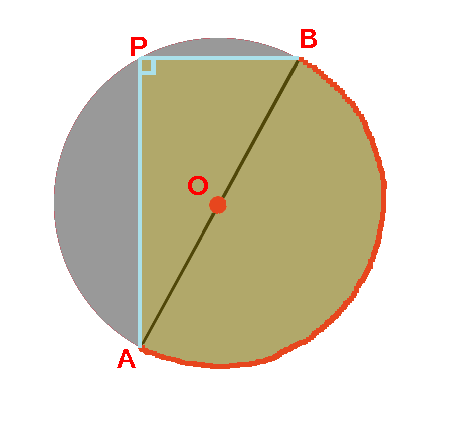
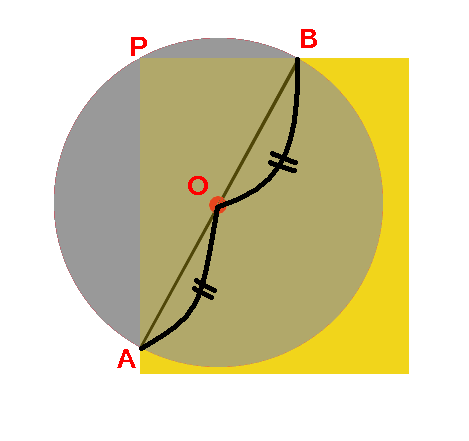
(※円で言えば半径ではなく直径に相等するものが,長軸・短軸なので,(1)の楕円の長軸の長さは 2a ,短軸の長さは 2b となる.) 長軸と短軸の交点を中心という.(1)の楕円の中心は原点 O( 0 , 0 ) にあ まず、内接円の中心(内心)を求めます。 性質②から、角の二等分線の交点を求めればよいですね。 角の二等分線は、各頂点からコンパスをとって弧を描き、弧と辺が交わる \(2\) 点からさらに弧を描き、その交点と頂点を直線で結べば作図できます。1、空き缶の円を紙に写し取ります。 2、紙に書いた円にピッタリと角が合うように 直角の物(ハガキなど)を置きます。 (Pの位置) 3、直角の物と円が交わる2点に印を付けます。 (AとB) 4、AとBを結んだ線の真ん中の点が、この円の中心になります。 (Oの点) 5、紙を空き缶に乗せて、求めた円の中心をクギなどで印を付ければできあがり!
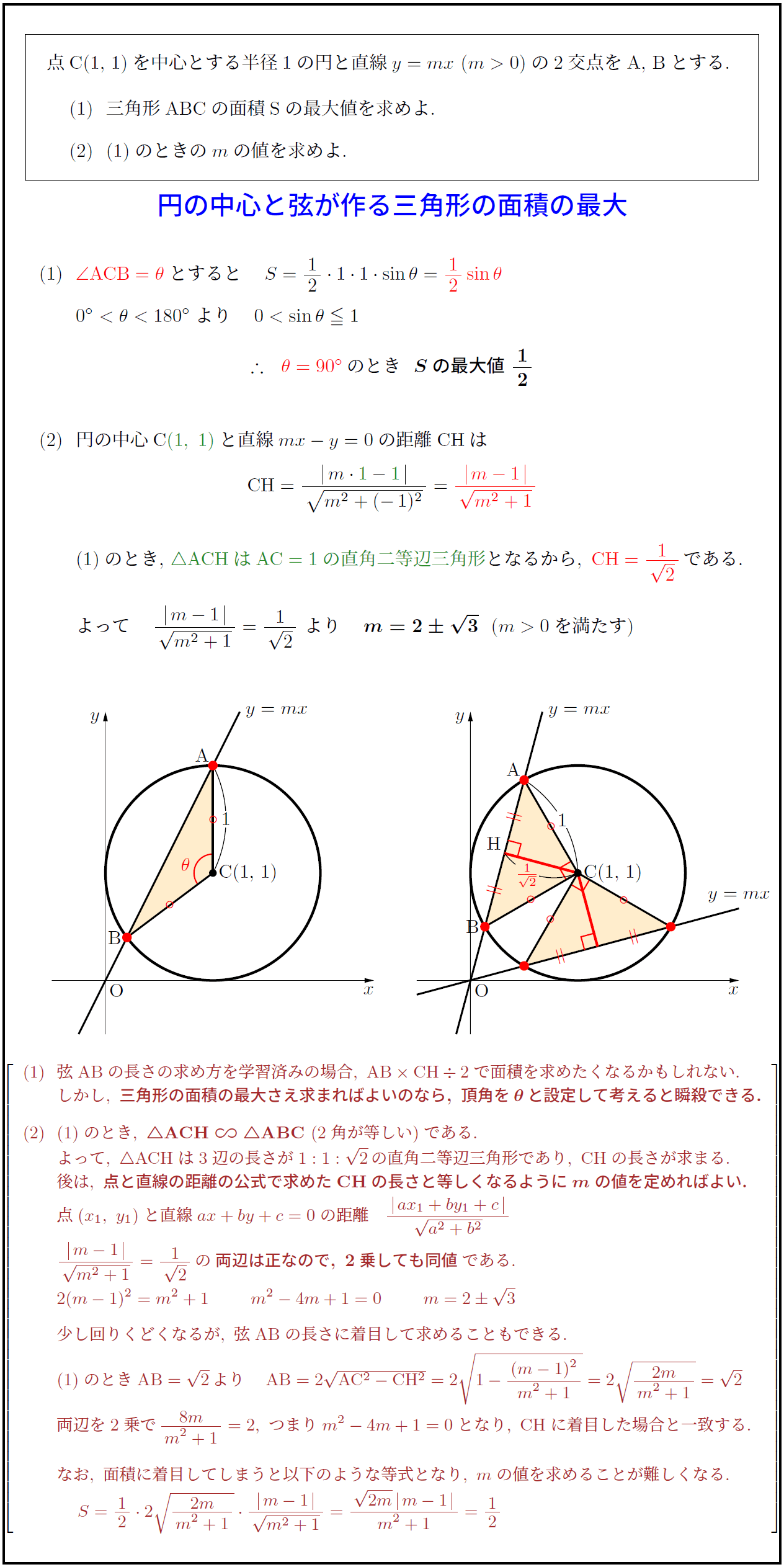



高校数学 円の中心と弦が作る三角形の面積の最大 受験の月



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座
こんにちは、ウチダショウマです。 今日は数学a「図形の性質」で習う 「三角形の外心(垂心)」 について、性質の証明や座標の求め方、位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心とは なぜ"外心"なのか、いきなり説明することは困難です。では,円の方程式の導き方を確認しましょう。 ここでは, 『「円周上の点」と「中心」の距離』と『半径』が同じ ということを利用して,円の方程式を導いてみます。 さらに,この式を展開して整理すると, x2 y2 2 ax 2 by a2 b2 r2 =0 となります。 これより,円の方程式は l,m,n を定数として, x2y2lxmyn=0・・・・・・ (2) (円の方程式は, (1)や (2)の形で 3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出する. 導出した式で計算フォームを作成. Excelにコピペして使えるフォーマットあり. 単純な「連立方程式」の問題ですが,一般解は少し複雑な形になります. 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




基本 円の方程式 なかけんの数学ノート
紙コップの円の中心を通る線が書けるのです。 1本の線では紙コップの円の中心は 特定できません。 そこで紙コップの向きを変え、 2本の線を引く事で 紙コップの円の中心を出す事が出来るのです。 今回この円の中心を 出す方法を使って工作したものがコレ。 これは同じ円に2つの角を並べてみるとよくわかりますよ。 図からもわかる通り、角は3点から作られていますが、 中心角と円周角は2点が共通している ことがわかると思います。(1)求めたい2つに"0"を入れる、空白にしない、ということをやられていない (2)あり得ない値を入れられている(例えば弦長のほうが弧長より長いなど) (3)入力するのは2つ、0にするのも2つなのを数が間違っている。 があります。ご確認ください。



1



家具製作資料 半径の判らない円弧半径の求め方 家具制作鯛工房
円の中心座標を適当に設定し、図2のように3点と中心の距離を求め、その距離の差を計算する。点1を通る円を作図しても、円は点1しか通らない。 図2 ソルバーを用いて3点を通る円を求める ツール→ソルバーをクリックし、ソルバーパラメータ設定画面を表示する。 目的セルを1番目の差に設定円の中心の求め方 三角定規でなくても良いのですが、直角部分を円の任意の箇所に置きます。 底辺と円の交差する点をa、もう一方の高さ部分と円の交差する点をbとし、aとbを直線で結びます。 その線にやや直角位になる様に三角定規を移動し、同じ方法2年生で学んだ四角形のココと 全く同じですね ・x=abc ( 四角形の外側の角) 《 例 》 円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45° xは3コマ分の中心角の半分 (=円周角) → x = 1 2



幾何計算 2点と半径から円の中心点を求めます Satoh




三角定規で円の中心を作図 おときち副塾長 電脳空間学習塾かもん Youtube
※ 円ならば右辺は半径の二乗なので 0 より大きな値になるはずです。 右辺の平方完成をすると、 となり、円の条件を満たします。 よって 中心の座標は p になります。 上で求めた中心 p の座標を p とおくと、 と は次のように表現できます。指定した3点を通る円の式 困っていたのでありがたいです。 計算過程も書いてあると尚嬉しいです。 タンクの中心からずれた位置へ差し込むパイプの長さを求めました。 半径rと x座標a,c,e から y座標b,d,f が求められればサイコーです! アンケートにご点 (−a ,−b) を中心とする半径 r の円の方程式が (xa) 2 (yb) 2 =r 2 点 (a ,−b) を中心とする半径 r の円の方程式が (x−a) 2 (yb) 2 =r 2 のように,中心の座標 (a , b) は,円の方程式では見かけ上の符号が逆になる点に注意. (1)(2)とも右辺は r 2 なので, 半径が 2 → 右辺は 4




おうぎ形の中心角の求め方を教えて下さい Clear



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく



3次元空間での円の中心の求め方 Inak Engineering Llc




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート




四角形の中心の求め方 四角形の中心 真中 の求め方は 各辺の真中を添付 Okwave



円中心点作図 円の中心を作図する問題ですどうやって作図するのですか Yahoo 知恵袋




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




円の中心を求める 3つの方法 Wikihow
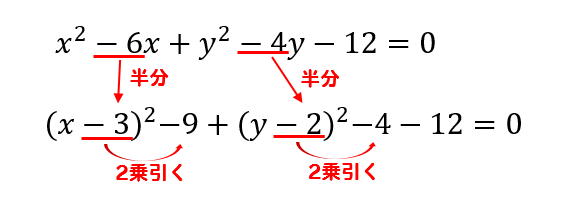



円の方程式 中心の座標と半径の求め方を解説 数スタ




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室



作図 円に内接する正三角形の作図方法とは 数スタ



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
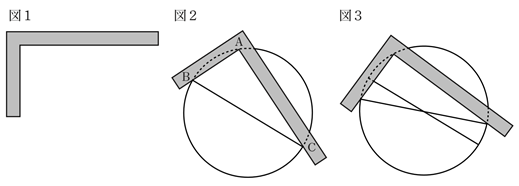



曲尺を使い円の中心を求める 1 準2級 カワズの数学ノート 数学検定 準2級



1




中1 作図 円の中心を求める方法を解説 数スタ




中1 作図 円の中心を求める方法を解説 数スタ



円の中心の求め方 Love金沢水彩画




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




円の中心を求める 3つの方法 Wikihow



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




3点を通る円を求める Qiita
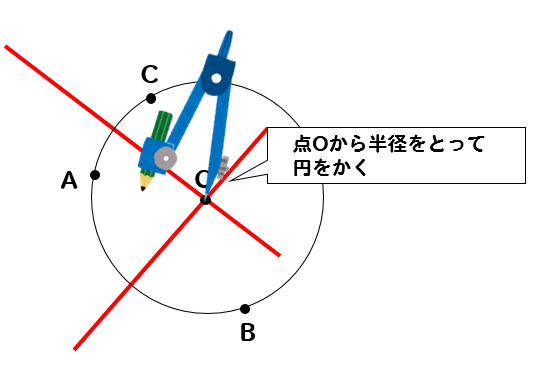



中1 作図 円の中心を求める方法を解説 数スタ




円の中心を求める 3つの方法 Wikihow




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ




最後の2円の中心間の距離の求め方が分かりません Clear




中心間の距離dの求め方を教えてください 数学aです よろしくお願いいたします Clear




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary



外接円 外心について
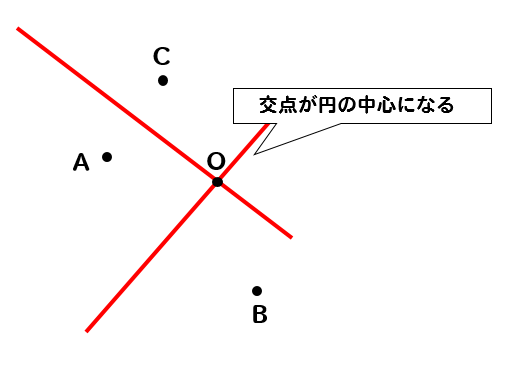



中1 作図 円の中心を求める方法を解説 数スタ




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト
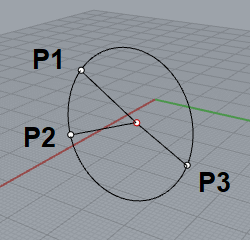



3次元空間での円の中心の求め方 Inak Engineering Llc




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の中心角の求め方 Youtube
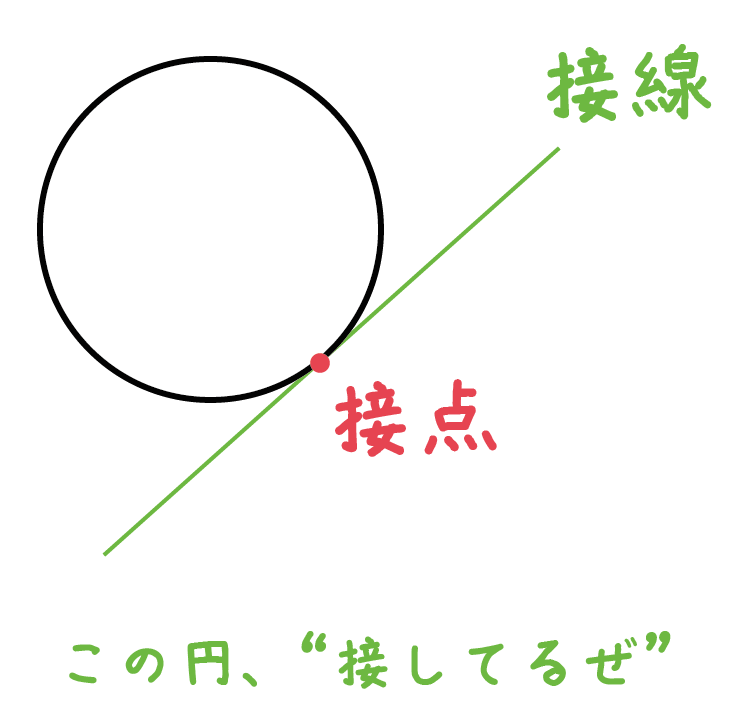



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



外接円 外心について




作図 05 円の中心の求め方 Youtube
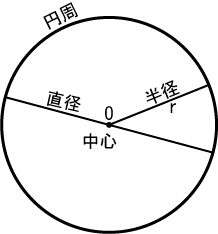



円 数学 Wikipedia




三角形の外心について知っておきたい知識まとめ 理系ラボ
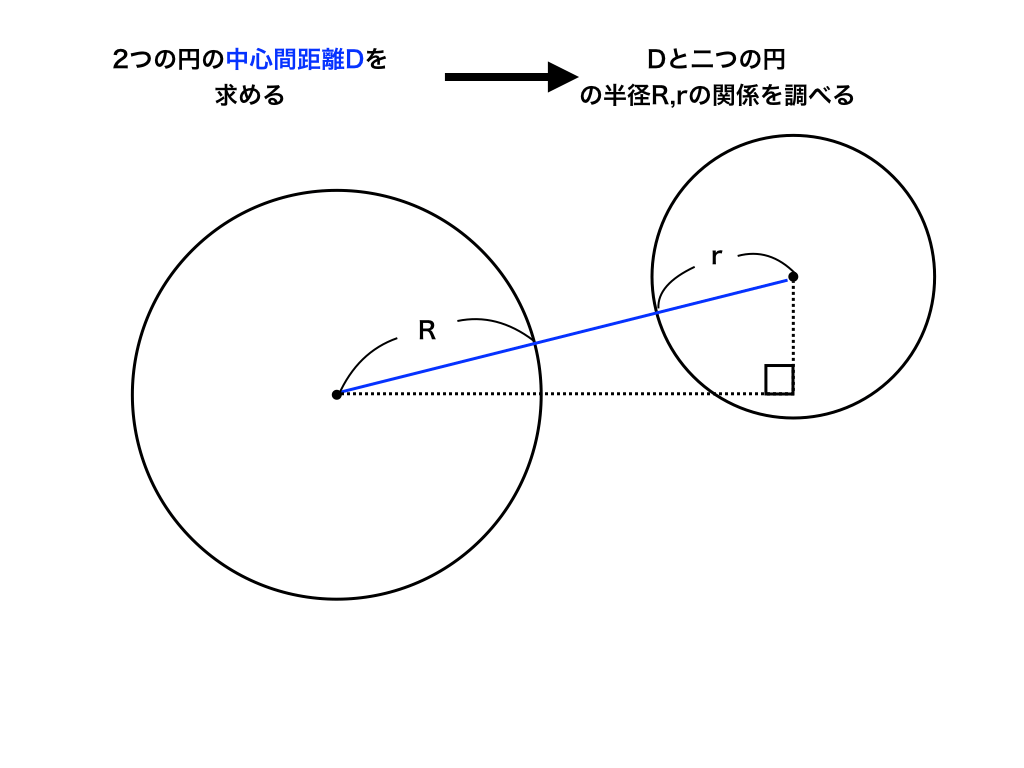



2つの円の位置関係と共通接線の求め方 図形と方程式 2



空き缶の中心の見つけ方 綿菓子を自宅で作ろう




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室



1




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



心に強く訴える円 中心 求め方 最高のぬりえ




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円の中心の出し方 コンパスなし 直径わからない編 シャンハイ山本弾工房




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト



高校数学b 円のベクトル方程式2パターン 受験の月



空き缶の中心の見つけ方 綿菓子を自宅で作ろう



中1 作図 円の中心を求める方法を解説 数スタ



中1 作図 円の中心を求める方法を解説 数スタ




心に強く訴える円 中心 求め方 最高のぬりえ




円の中心を求める 3つの方法 Wikihow




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




円の中心を求める 3つの方法 Wikihow




この問題の の中点の座標の求め方を教えて下さい 至急です Clear




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



From灘 円の中心の求め方 朝日小学生新聞 中学受験eye 関西圏



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




3点を通る円を求める Qiita
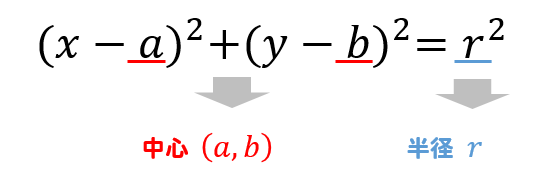



円の方程式 中心の座標と半径の求め方を解説 数スタ



3点を通る円の中心と半径 Notes Jp




中1 作図 円の中心を求める方法を解説 数スタ
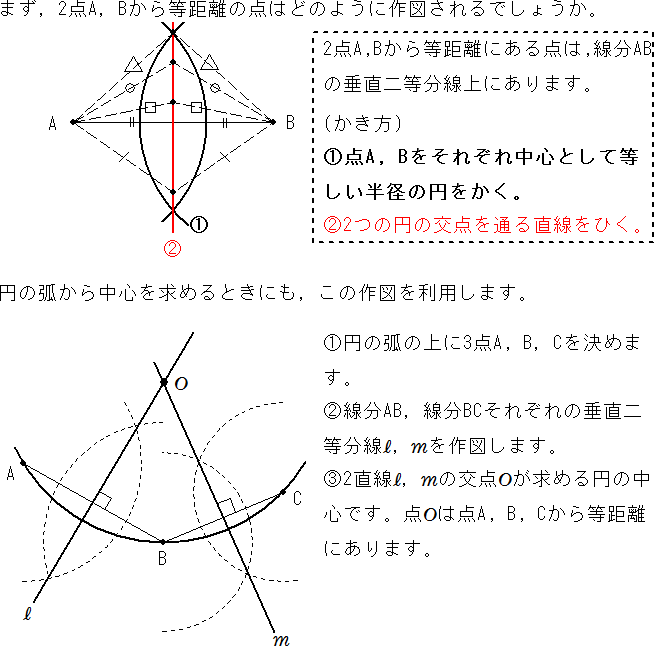



平面図形 円の中心を求める作図 中学数学 定期テスト対策サイト




高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




円の中心を求める 3つの方法 Wikihow



1




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest




1数 作図による円の中心の求め方 Youtube




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア
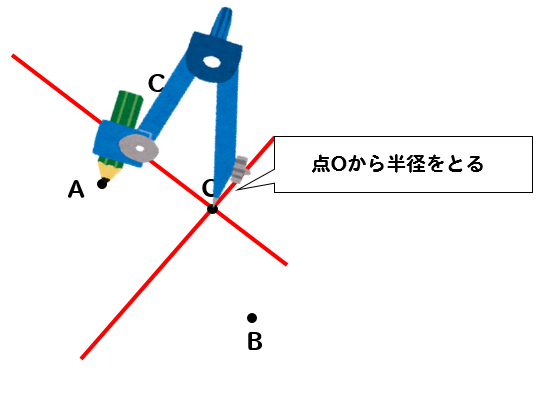



中1 作図 円の中心を求める方法を解説 数スタ




2つの点から円の方程式を求める 数学ii By Okボーイ マナペディア




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中1 作図 円の中心を求める方法を解説 数スタ



中1 作図 円の中心を求める方法を解説 数スタ



Studydoctor円の公式と なぜ 中学1年数学 Studydoctor



0 件のコメント:
コメントを投稿