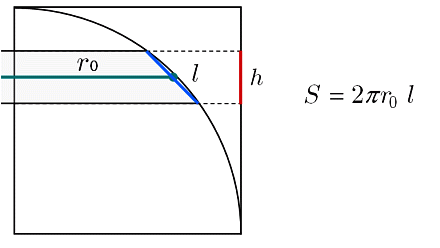
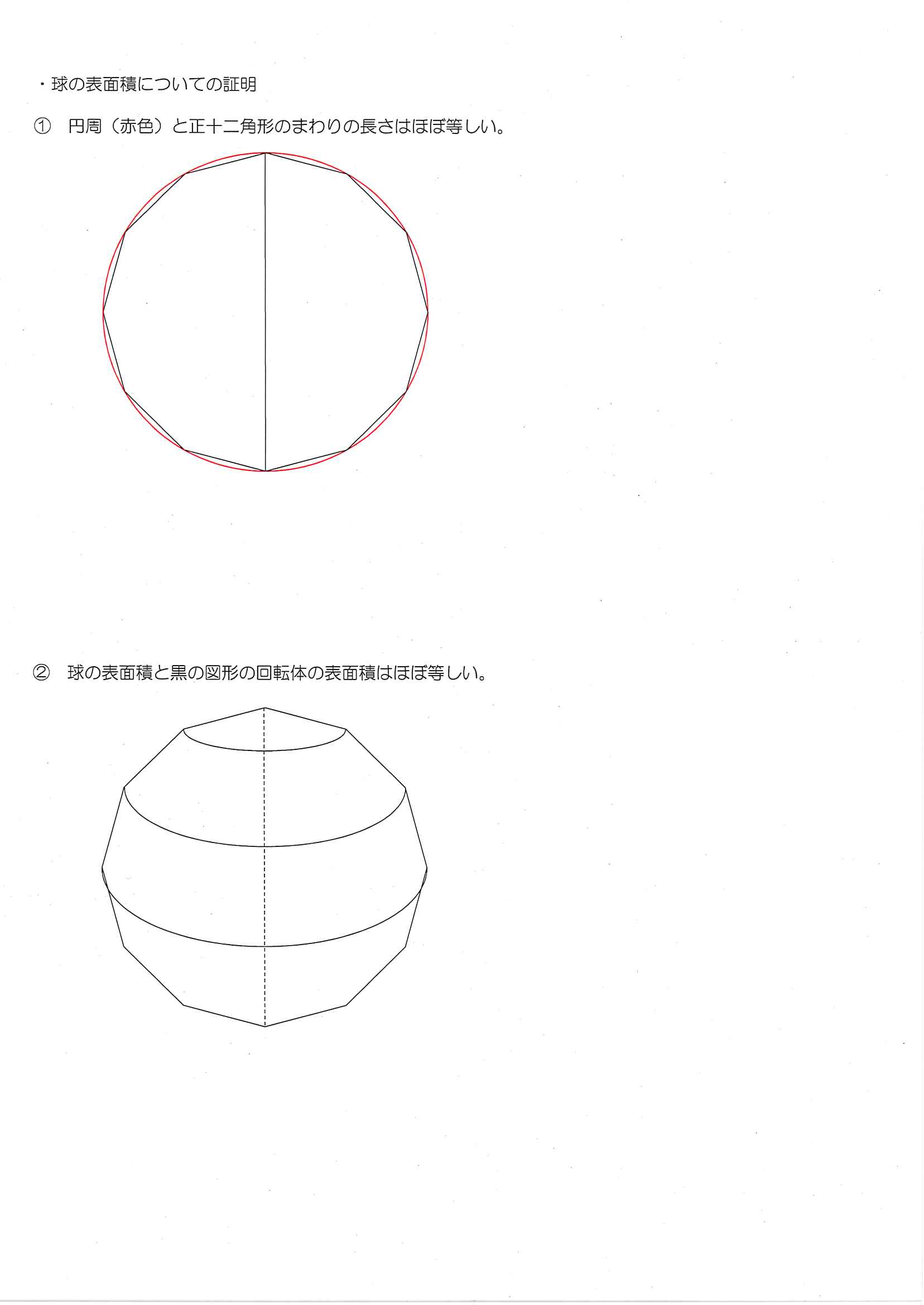
表面積の求め方の基本、さいごは球の表面積です。 例題4の立体は半径 \(\frac{3}{2}\) cmの球になります。 ただ球の表面だけは、展開図のように平らに伸ばすことができません(ミカンの皮を一回でむいてテーブルに置いても、しわくちゃになる)。球の表面積がそれに接する円柱の側面積に等しいのは、微小部分を円柱に投影したとき 任意の位置でスライスした(正確な半球でないもの)場合の表面積の求め方 を 上記では、球冠の側面積を重積分で求めたが、高校の数学Ⅲの範囲で十分求めよって、球の体積Vは、円の面積をx 方向に積分すると、V=2∫0rπ(r2-x2) dxより、 V=2πr2x-(x3/3)0r=(4/3)πr3を導くことができる。 ②球の表面積の公式の求め方(1)

球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
数学 球 表面積 求め方
数学 球 表面積 求め方-R r の球の表面積は S=4\pi r^2,\ S = 4πr2, 球の体積は V=\dfrac {4} {3}\pi r^3 V = 34 πr3 である。 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するための



1
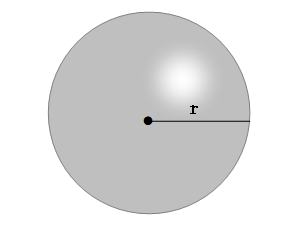
半径を使って直径や円周、体積、表面積を求める公式を学びましょう。 D = 2r 円 と同様に、球の直径は半径の2倍です。 C = πD か 2πr 円 と同様に、球の周長は直径にπをかけたものです。球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球の表面積の公式 半径 r の球の表面積を S とすると、 \begin {align}\color {red} {S = 4\pi r^2}\end {align} 表面積は r (半径)を 2 回かけるのがポイントです。
求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方 半径 の球の表面積を とおくS:球の表面積ってどうやって求めるのだろう。 s:円の場合は細かな三角形に分割して面積を求めたよ。 円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。 s:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。 中1数学「球の表面積と体積の求め方」練習問題有についてまとめています。 球の表面積と体積は、入試や定期テストでもよく出題される単元です。 しかしながら、テスト本番で、公式を思い出せなかったということも少なくないです。 何度も問題を解い
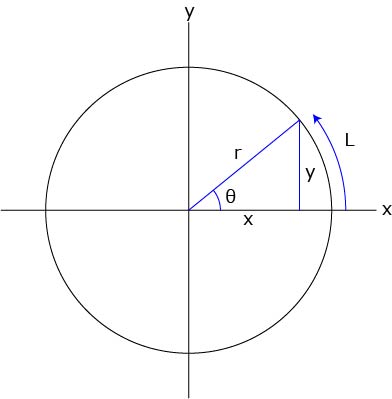
なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。(球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。 球の体積 は、 身の上に心配あるので、参上。 球の表面積は、心配球の体積は \(\dfrac{4}{3}{\pi}r^{3}\) となります。 語呂合わせとして有名なのが、 「身の上に心配あるので参上」 です。 分母の3の上に分子の4があることを「身(3)の上に心(4)~」という言葉で表しており、とても上手い語呂合わせとなっています。 「心配ある」という部分は表面積の公式と
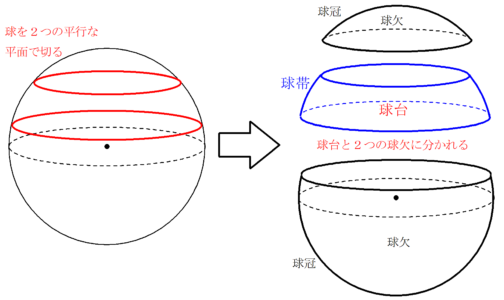



球台と球帯 Fukusukeの数学めも



球の表面積 体積の教え方
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半#球 #表面積 #中学受験 #算数球の表面積の求め方の動画です。パート1 https//youtube/pgQPXMCCHIcパート2 https//youtube立体角は、半径1の球(単位球)の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。 「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。 立体角の計算例




球の求め方教えてください Clear




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.N次元球の表面積と体積の求め方。 こちらでで触れたガンマ関数(Γ Function)の応用例。 Python演算処理階乗と順列と組み合わせ 正直私にとってはパラダイムシフトでした。半径 r の球の表面積は、次の式で求められます。 球の表面積 \begin{align*} S = 4\pi r^2 \end{align*} 表面積 = 4 × 314 × 半径 × 半径 公式の導出方法と計算例については、「球の表面積の求め方」をご覧
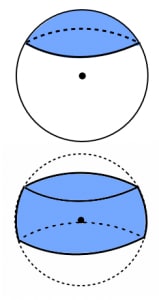



球欠 球台の体積と球冠 球帯の表面積 高校数学の美しい物語




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
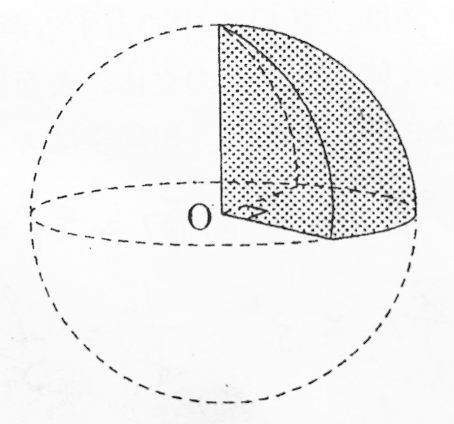
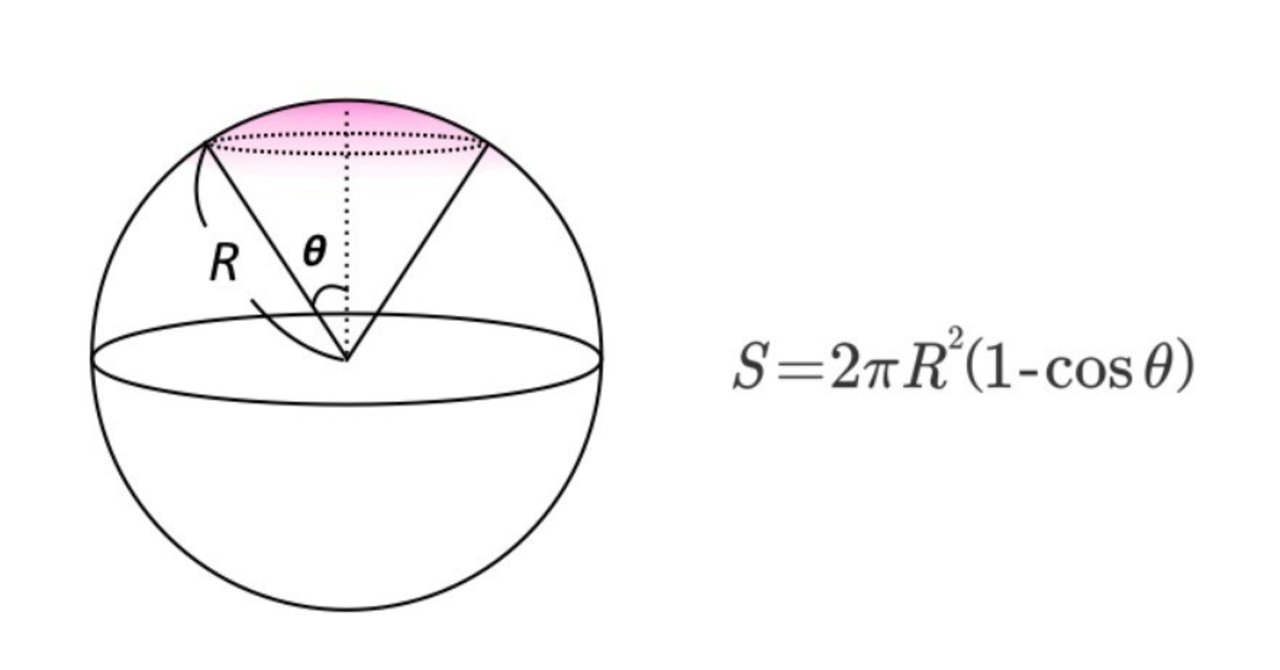
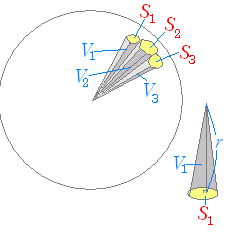
球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、 \begin{equation} \frac{1}{2}\cdot 4\pi R^2=2 \pi R^2 \end{equation} となるので、確かに球冠の面積の公式で求めた結果と一致しています。 では、こちらも証明に入っていきます。球を平面で切り取った立体の体積,および側面の面積の求め方を解説します。 結果を覚える必要はありませんが,導出方法はマスターしておきましょう。 目次 球を切って得られる立体の名前 球欠,球台の体積 球冠,球帯の表面積比表面積(ひひょうめんせき、英語:specific surface area)とは、ある物体について単位質量あたりの表面積または単位体積あたりの表面積のことである。 界面に関する学問、界面化学やコロイド化学、あるいは触媒化学などで主に使われる指標である。 触媒を用いたガス吸着など、表面の物理的



球の表面積の公式の求め方




球の表面積と体積を求める方法 中学数学 By じょばんに マナペディア
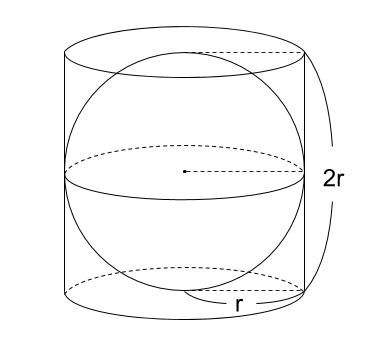
円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事球の体積の考え方の例 -πr³ 球の表面積の考え方の例 4πr² 4 3 円がぴったり 入る円柱 円がぴったり 入る円柱 球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める球の体積を半径で微分すると球の表面積になり、球の表面積を積分すると球の体積になると習ったときは感動しました。 4/3πr^3 ⇒ 4πr^2 微積分を習うのは高校なので、球の体積や表面積の求め方を習ったのも高校だと思います。
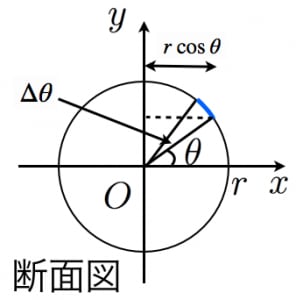



球の体積と表面積を積分で証明 高校数学の美しい物語
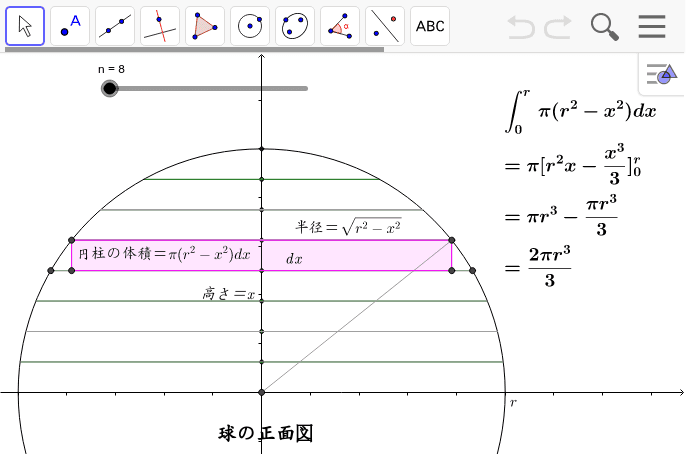



球の体積の積分 Geogebra
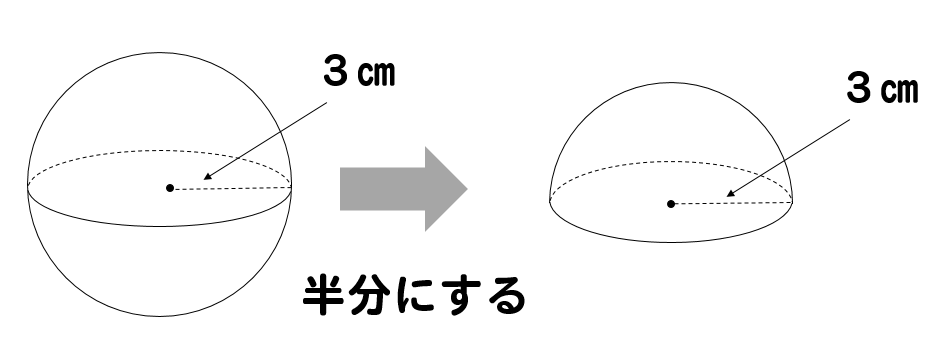
半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め4.実験の原理 球の体積測定 水で満たしたバケツに球を沈めたとき,押しのけた水の量が球の体積である 球の表面積測定 球の表面を覆うように巻き付けたロープを面積が求められる他の図形に敷き詰めたとき, その面積が球の表面積である 円のように見えないこともないので,この図形を円と捉えることにする. 円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立てて面積を求めると, 面積= 1




球体の表面積 積分で求める方法 うちーノート




球の表面積と体積の公式 数学fun



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球表面積積分 球的表面積的求法 Dycvi



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の体積 球の表面積の公式の導出 積分 優技録



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



1



大学入試問題




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




定積分と面積3 球の表面積 Youtube




球の表面積の公式について みたにっき はてな



初等幾何 球の表面積を求める 大人が学び直す数学




球の体積と表面積 公式と計算問題と証明 Irohabook




球の表面積の求め方 公式と計算例




球の表面積と円の面積 球の表面積や円の面積を積分により求める場合 パラメ Okwave



Math 円柱 内接する球 円錐の体積と表面積 働きアリ




初等幾何 球の表面積を求める 大人が学び直す数学




表面積の求め方 計算公式一覧




球の体積 表面積の求め方 公式 小学生 中学生の勉強



なぜ球の体積は Math Frac43 Pi R 3 Math なのでしょうか Quora



Sphere 01




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の問題 苦手な数学を簡単に




球の表面積と体積の公式 数学fun




球の表面積 Sgk Note




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



中1数学 球の表面積と体積の定期テスト過去問分析問題 Atstudier




球帯の定理 感じる科学 味わう数学




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




Mathematics 球の体積と表面積を求める公式 働きアリ




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



1
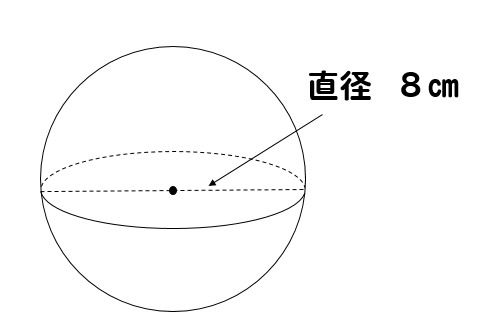



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の表面積と体積の公式 数学fun



Juusekibun



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の体積と表面積 Youtube



数学 球の表面積を積分で計算してもうまくいかない人へ




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球の表面積の求め方 その3 感じる科学 味わう数学




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋




中1数学 球 例題編 映像授業のtry It トライイット



球の表面積の計算 もう一つの方法




球の表面積と体積の公式 数学fun
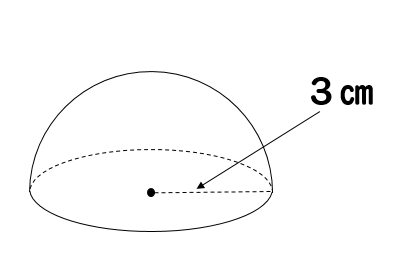



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



研究




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ



球体の表面積を 積分で求めて下さい 塾で積分を習ったのですが そのとき 球 Yahoo 知恵袋




球の表面積の公式について みたにっき はてな




球の体積公式の微分が表面積になっている理由 Youtube
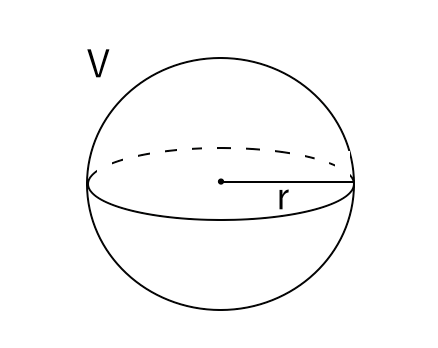



球の表面積と体積の求め方 苦手な数学を簡単に
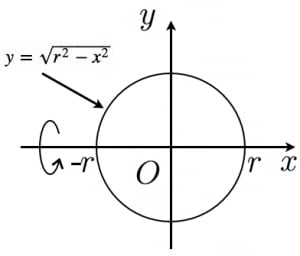



球の体積と表面積を積分で証明 高校数学の美しい物語




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ
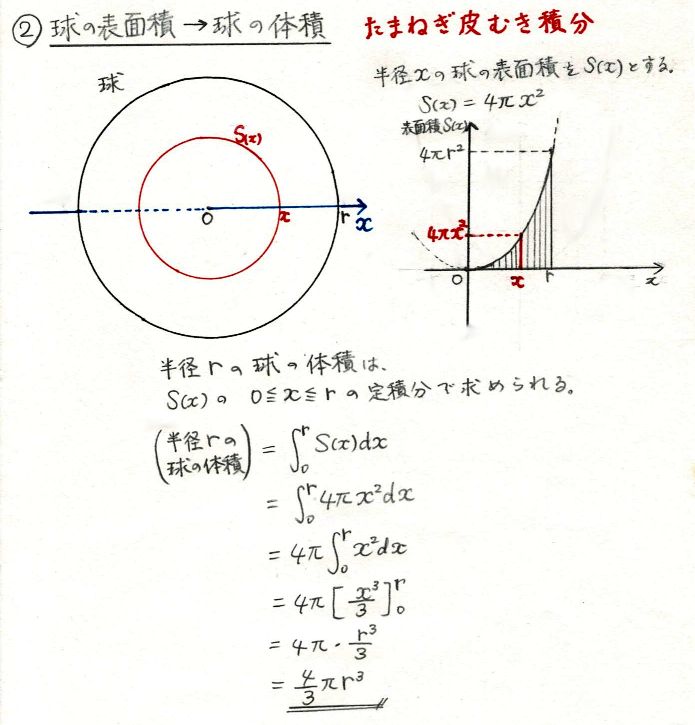



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋
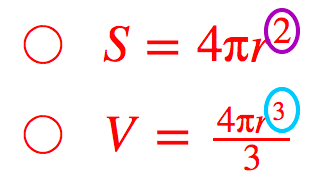



球の表面積と体積の求め方 苦手な数学を簡単に




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球帯と球冠




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



数学 球の表面積を積分で計算してもうまくいかない人へ




中1 数学 6 5 球の体積 表面積 Youtube




半球の体積と表面積を計算する 具体例で学ぶ数学



3




球の表面積 体積 身勝手な主張




球の表面積と体積の公式 数学fun
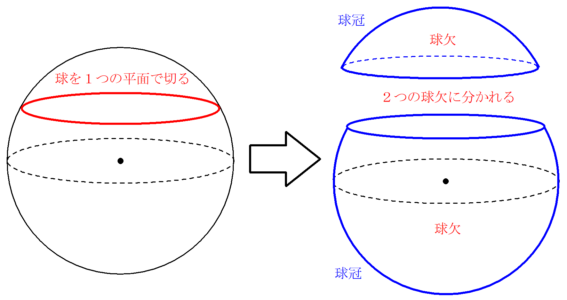



球欠と球冠 Fukusukeの数学めも



Math 球の体積と表面積を求める公式 働きアリ The 2nd




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




スタディピア 立体の表面積



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



数学 球の表面積を積分で計算してもうまくいかない人へ



球の表面積の求め方 中学受験塾act アクト のブログ




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の体積 表面積 無料で使える中学学習プリント




回転体の表面積 側面積 身勝手な主張




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館



28で見込む部分の球の表面積の計算 Matsubayashi Note




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



1




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



例題対比 球の体積と表面積



ベクトルポテンシャル補足 12 での 球の表面積 を求める証明 Jo3krpの独り言



球の表面積の公式の求め方



0 件のコメント:
コメントを投稿